Convolution Neural Network
Overview
Among the various deep learning models such as stacked auto-encoders [1], deep Boltzmann machines [2], deep conventional extreme learning machines [3], deep belief networks [4], etc., CNN based models are the most powerful for image segmentation. CNNs were introduced by Fukushima et al. [5] as a self-organizing neural network (Neocognition) that uses the hierarchical receptive field of the visual cortex. Later, Waibel et al. [6] and LeCun et al. [7] proposed shared weights approach (forward propagation) and parameters tuning (backpropagation) for phoneme recognition and document recognition respectively. The main advantage of CNNs over MLP is that shared weights in the network significantly reduces the number of trainable parameters without the degradation of the performance.
Generally, CNNs involve three types of layers: convolution, activation, and pooling. The sequence of these layers forms a complete model, where each unit is compiled from the weights of the neighbouring units to form continuously increasing wider receptive field [8]. Finally, similar to the MLP, the class probabilities are predicted by applying softmax activation in the output layer and the network is trained to minimize the loss or objective function. Following from these notions, many state-of-the-art CNN models are developed like AlexNet [9], VGGNet [10], ResNet [11], GoogLeNet [12], MobileNet [13], DenseNet [14], etc., to address the wide variety of tasks in deep learning.
Convolution Layer
In the convolution layer, feature maps are generated by convolving the kernel or filter of trainable parameters (weights) with the input, to highlight and learn complex representations. The convolution operation requires to set certain hyperparameters like kernel size, number of filters, and amount of padding (number of pixels added around the image before convolution) and strides (by how many pixels the kernel should slide). To the best of our knowledge, height and width dimensions of the input feature maps are always kept the same and kernel size is always set as an odd number to offer symmetry around the output pixels. With continuous advancements, many variants of convolution layers have been proposed like atrous convolution [15], transposed convolution [16], depthwise separable convolution [17], spectral convolution [18], inception convolution [19], etc., for various application areas. All these convolution variations are most widely used in the segmentation approaches.
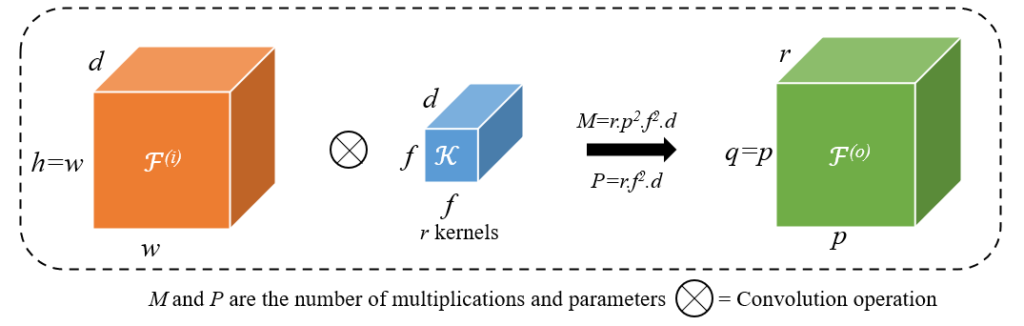
Fig. 1 presents the standard 2D convolution operation along with the number of parameters and multiplications incurred for some input feature map, ![]() , with width
, with width ![]() , height
, height ![]() and depth
and depth ![]() , to generate output feature map,
, to generate output feature map, ![]() , where dimension
, where dimension ![]() . The output dimension,
. The output dimension, ![]() can be computed prior to the convolution operation using Eq.1. Eq.2 presents the mathematical formulation of the convolution operation with a kernel or a filter,
can be computed prior to the convolution operation using Eq.1. Eq.2 presents the mathematical formulation of the convolution operation with a kernel or a filter, ![]() , where
, where ![]() represents the kernel size,
represents the kernel size, ![]() indicates number of filters and
indicates number of filters and ![]() is depth of the kernel, same as input.
is depth of the kernel, same as input.
(1) ![]()
where ![]() and
and ![]() denotes the amount of strides with range as a set of positive integers (
denotes the amount of strides with range as a set of positive integers (![]() ) and padding as a set of natural numbers (
) and padding as a set of natural numbers (![]() ) respectively.
) respectively.
(2) 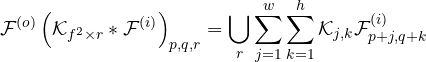
where ![]() indicates the convolution operation is performed
indicates the convolution operation is performed ![]() times, where each output is concatenated along the depth axis.
times, where each output is concatenated along the depth axis.
It can be observed that for 3D input and 3D filter, the operation is termed as 2D convolution, this is because the depth of the filter is same as input, and filter slides in two dimensions (horizontally and vertically). However, the same operation can also be extended to perform 3D convolutions for 3D volumes, especially in the biomedical imaging. Hence, for some 3D volume, ![]() , the convolution can be formulated using Eq.2, by appending another dimension as shown in Eq.3, and also the corresponding output dimension can be computed similarly to 2D.
, the convolution can be formulated using Eq.2, by appending another dimension as shown in Eq.3, and also the corresponding output dimension can be computed similarly to 2D.
(3) 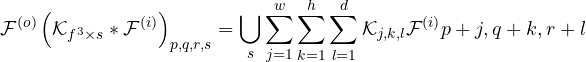
where ![]() indicates the extracted feature maps using s number of 3D kernels,
indicates the extracted feature maps using s number of 3D kernels, ![]() .
.
Activation Layer
The activation layer tends to add non-linearity in the learning process by applying certain functions [20] on the input feature maps. The added non-linearity aids in discovering and learning more complex patterns in the subsequent convolution layers. Besides, it is observed that an ideal activation function must possess the following features for optimal learning in the deep learning models:
- Avoid activation shift to 0: If the value of activation lies between 0 and 1 then eventually the activation gradient will converge to zero and there will not be any more learning in the model. This is popularly known as the vanishing gradient problem. For instance, this problem may occur in deep networks that have sigmoid or tanh activations in the hidden layer (between the input and output layer) of the network. This is because sigmoid and tanh squeeze the activations in the defined range
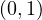 and
and 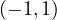 respectively. Therefore, these activations are rarely used in the hidden layer but can be utilized in the output layer for binary classification.
respectively. Therefore, these activations are rarely used in the hidden layer but can be utilized in the output layer for binary classification. - Symmetric: The activation function should be zero centered i.e. symmetric around the origin. This is because the gradient of the activation function, computed during backpropagation, should not get shifted to a particular direction.
- Computation: Since activation functions are associated with every layer to add non-linearity, these should be made computationally inexpensive.
- Differentiable: The activations should have continuous nature so that the output of every layer is differentiable at every point during backpropagation.
Ramachandran et al. [21] presented popular non-linear activations that are employed in the deep learning models along with its respective advantages and disadvantages. The activation functions such as sigmoid, tanh, ReLU and its variants, are most common among the popular deep learning models. However, it is observed that no activation function matches the properties concerning the ideal activation function, thereby leaving the further scope of development and enhancement to contribute in this area of deep learning.
Pooling Layer
Followed from the convolution and activation layer, the pooling layer applies statistical transformations (mean, average, max, etc.) to the feature maps which induces the translation invariance in the model. The primary goal of this layer is to reduce the dimension of the input feature to speed up the computation without the involvement of any weights or training parameters. This layer requires two hyperparameters, window size (![]() ) and amount of stride (
) and amount of stride (![]() ), where values of
), where values of ![]() and
and ![]() are generally kept 2. For some feature map,
are generally kept 2. For some feature map, ![]() , the
, the ![]() pooling operation (
pooling operation (![]() ) can be presented with Eq.4, to produce output feature map,
) can be presented with Eq.4, to produce output feature map, ![]() , and the corresponding output dimensions,
, and the corresponding output dimensions, ![]() can be computed using Eq.5. Akhtar et al. [22] recently presented a detailed review on the various pooling variants classified based on value, probability, domain transformation and rank. However, in the deep learning models, most widely used pooling approaches are max pooling and average pooling, where max pooling aims to preserve the high intensity feature values and average pooling preserves the mean of intensity values. Besides, it depends on the feature distribution and task requirement to opt for a certain type of pooling operation.
can be computed using Eq.5. Akhtar et al. [22] recently presented a detailed review on the various pooling variants classified based on value, probability, domain transformation and rank. However, in the deep learning models, most widely used pooling approaches are max pooling and average pooling, where max pooling aims to preserve the high intensity feature values and average pooling preserves the mean of intensity values. Besides, it depends on the feature distribution and task requirement to opt for a certain type of pooling operation.
(4) ![]()
(5) ![]()
References
- Yoshua Bengio, Pascal Lamblin, Dan Popovici, and Hugo Larochelle. 2007. Greedy layer-wise training of deep networks. In Advances in neural information processing systems. 153–160.
- Ruslan Salakhutdinov and Geoffrey Hinton. 2009. Deep boltzmann machines. In Artificial intelligence and statistics. 448–455.
- Qin-Yu Zhu, A Kai Qin, Ponnuthurai N Suganthan, and Guang-Bin Huang. 2005. Evolutionary extreme learning machine. Pattern recognition 38, 10 (2005), 1759–1763.
- Geoffrey E Hinton, Simon Osindero, and Yee-Whye Teh. 2006. A fast learning algorithm for deep belief nets. Neural computation 18, 7 (2006), 1527–1554.
- Kunihiko Fukushima and Sei Miyake. 1982. Neocognitron: A self-organizing neural network model for a mechanism of visual pattern recognition. In Competition and cooperation in neural nets. Springer, 267–285.
- Alex Waibel, Toshiyuki Hanazawa, Geoffrey Hinton, Kiyohiro Shikano, and Kevin J Lang. 1989. Phoneme recognition using time-delay neural networks. IEEE transactions on acoustics, speech, and signal processing 37, 3 (1989), 328–339.
- Yann LeCun, Léon Bottou, Yoshua Bengio, and Patrick Haffner. 1998. Gradient-based learning applied to document recognition. Proc. IEEE 86, 11 (1998), 2278–2324.
- Wenjie Luo, Yujia Li, Raquel Urtasun, and Richard Zemel. 2016. Understanding the effective receptive field in deep convolutional neural networks. In Advances in neural information processing systems. 4898–4906.
- Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. 2012. Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems. 1097–1105.
- Karen Simonyan and Andrew Zisserman. 2014. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556 (2014).
- Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2016. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition. 770–778.
- Christian Szegedy, Wei Liu, Yangqing Jia, Pierre Sermanet, Scott Reed, Dragomir Anguelov, Dumitru Erhan, Vincent Vanhoucke, and Andrew Rabinovich. 2015. Going deeper with convolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition. 1–9.
- Andrew G Howard, Menglong Zhu, Bo Chen, Dmitry Kalenichenko, Weijun Wang, Tobias Weyand, Marco Andreetto, and Hartwig Adam. 2017. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv preprint arXiv:1704.04861 (2017).
- Gao Huang, Zhuang Liu, Laurens Van Der Maaten, and Kilian Q Weinberger. 2017. Densely connected convolutional networks. In Proceedings of the IEEE conference on computer vision and pattern recognition. 4700–4708.
- Liang-Chieh Chen, George Papandreou, Florian Schroff, and Hartwig Adam. 2017. Rethinking atrous convolution for semantic image segmentation. arXiv preprint arXiv:1706.05587 (2017).
- Dongseok Im, Donghyeon Han, Sungpill Choi, Sanghoon Kang, and Hoi-Jun Yoo. 2019. DT-CNN: Dilated and transposed convolution neural network accelerator for real-time image segmentation on mobile devices. In 2019 IEEE International Symposium on Circuits and Systems (ISCAS). IEEE, 1–5.
- François Chollet. 2017. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition. 1251–1258.
- Oren Rippel, Jasper Snoek, and Ryan P Adams. 2015. Spectral representations for convolutional neural networks. In Advances in neural information processing systems. 2449–2457.
- Narinder Singh Punn and Sonali Agarwal. 2020. Inception U-Net Architecture for Semantic Segmentation to Identify Nuclei in Microscopy Cell Images. ACM Transactions on Multimedia Computing, Communications, and Applications (TOMM) 16, 1 (2020), 1–15.
- Bekir Karlik and A Vehbi Olgac. 2011. Performance analysis of various activation functions in generalized MLP architectures of neural networks. International Journal of Artificial Intelligence and Expert Systems 1, 4 (2011), 111–122.
- Prajit Ramachandran, Barret Zoph, and Quoc V Le. 2017. Searching for activation functions. arXiv preprint arXiv:1710.05941 (2017).
- Nadeem Akhtar and U Ragavendran. 2020. Interpretation of intelligence in CNN-pooling processes: A methodological survey. Neural Computing and Applications (2020), 1–20.
