Blog

You are currently viewing KANs: The Future of Neural Networks? Exploring the Power of Learnable Activations

KANs: The Future of Neural Networks? Exploring the Power of Learnable Activations

The Kolmogorov-Arnold Representation Theorem

The foundation of KANs lies in the Kolmogorov-Arnold Representation Theorem (KART). This theorem states that any continuous multivariate function can be represented as a superposition of univariate functions:

\[f(x_1, …, x_n) = \sum_{q=0}^{2n} \Phi_q \left( \sum_{p=1}^n \phi_{q,p}(x_p) \right)\]

where \Phi_q and \phi_{q,p}(x_p) are continuous univariate functions. This theorem implies that we don’t necessarily need complex, high-dimensional functions to represent complex relationships; instead, we can use compositions of simpler, one-dimensional functions.

KAN Architecture

KANs leverage this idea by replacing the traditional weighted connections in neural networks with learnable univariate functions.

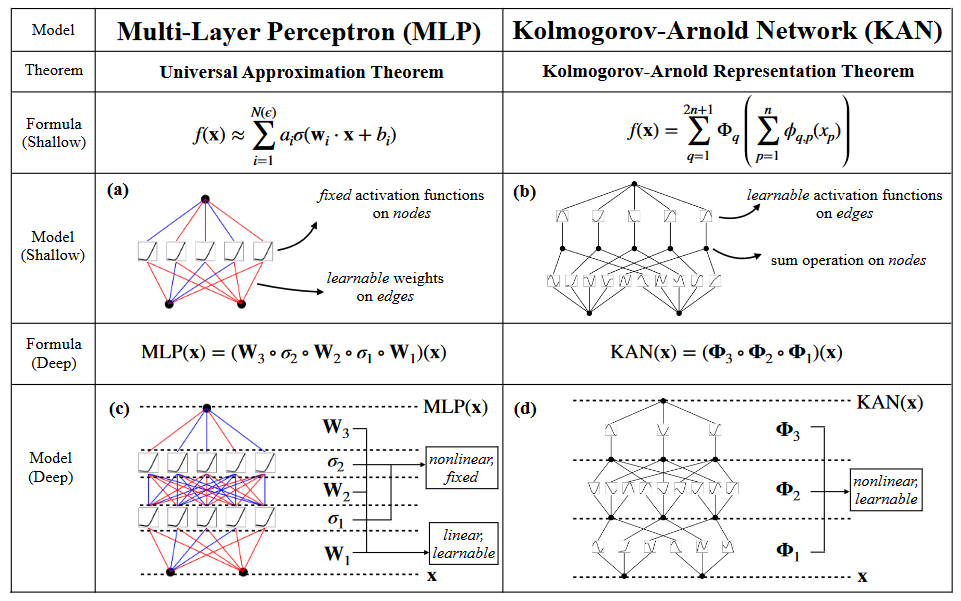
A KAN consists of:

  • Nodes: These perform summation operations, similar to nodes in traditional neural networks. However, they don’t apply any activation functions.
  • Edges: Each edge houses a learnable univariate function (often parameterized as a spline). These functions act as the “weights” of the network, determining how the signal from one node is transformed before reaching the next.

Mathematical Representation

A layer in a KAN can be mathematically represented as:

\[y_i = \sum_{j=1}^n \phi_{i,j}(x_j)\]

where x_j is the input to node j, y_i is the output of node i, and \phi_{i,j} is the learnable function associated with the edge connecting nodes j and i.

How Output is Calculated

  1. Input Transformation: Each input x_j is passed through its corresponding learnable function \phi_{i,j}. This function can be any continuous univariate function, but in practice, it’s often parameterized as a spline for flexibility and efficiency.
  2. Weighted Summation: The transformed inputs from all the neurons in the previous layer are summed together. The learnable functions act as weights, modulating the contribution of each input to the final output.
  3. Output: The resulting sum is the output y_i of the i-th neuron in the current layer.

Input Transformation: Each input x_j is passed through its corresponding learnable function \phi_{i,j}. This function can be any continuous univariate function, but in practice, it’s often parameterized as a spline for flexibility and efficiency.

Key Points

  • No Activation Function: Unlike traditional neural networks, KANs do not apply any fixed activation function (e.g., ReLU or sigmoid) after the summation. The learnable functions themselves introduce non-linearity.
  • Learnable Weights: The key innovation of KANs is that the “weights” (\phi_{i,j}) are not fixed parameters; they are learnable functions that are adjusted during training.
  • Stacking Layers: Multiple KAN layers can be stacked to create deeper networks. In this case, the output of one layer becomes the input to the next layer.

Why KANs?

  1. Interpretability: The use of univariate functions makes KANs more interpretable than traditional neural networks. We can visualize these functions to understand how each feature contributes to the final output.
  2. Efficiency: KANs have fewer parameters than traditional neural networks, making them computationally efficient.
  3. Accuracy: KANs have demonstrated competitive or even superior performance compared to traditional neural networks on various tasks, including function approximation and partial differential equation solving.

Challenges and Future Directions

  • Training: Training KANs can be computationally challenging, especially for deep networks. Efficient algorithms for training KANs are an active area of research.
  • Generalization: It’s not yet clear how well KANs generalize to complex, real-world problems. More research is needed to explore their capabilities on diverse tasks.
  • Hybrid Models: Combining KANs with other types of neural networks (e.g., convolutional or recurrent networks) could potentially lead to even more powerful and interpretable models.

Conclusion

KANs represent a significant departure from the traditional neural network paradigm. Their unique architecture, inspired by the Kolmogorov-Arnold Representation Theorem, offers promising advantages in terms of interpretability, efficiency, and potentially accuracy. While they are still in their early stages of development, KANs hold the potential to revolutionize the field of deep learning.

If you are interested in learning more about KANs, I encourage you to check out this awesome repository: https://github.com/mintisan/awesome-kan

Reserach paper: https://arxiv.org/pdf/2404.19756

Tags: ,

Leave a Reply