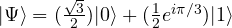Quantum Computing Part 1 - Punn's Deep Learning Blog

This post introduces the fundamental concepts that differentiate quantum computing from classical computing, primarily focusing on the shift from classical bits to quantum bits (qubits) and the implications of this change.

Classical vs. Quantum Bits

Classical computers operate using bits, which can exist in one of two distinct states: 0 or 1.
These states can be visualized as a switch being either off or on.
In contrast, quantum computers utilize qubits, which can exist in a superposition of both states simultaneously.
This means a qubit can be both 0 and 1 at the same time, unlike a classical bit.
This concept of superposition is crucial to the potential power of quantum computing.

Superposition and Measurement

Superposition allows quantum computers to perform calculations on a vast number of states concurrently.
Imagine a qubit as a sphere, where the north pole represents the state 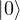$| 0 \rangle$ and the south pole represents $| 1 \rangle$ .
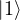A qubit in superposition can be any point on the sphere’s surface, representing a combination of both 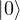$| 0 \rangle$ and $| 1 \rangle$ .
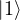This ability to explore multiple possibilities simultaneously is what potentially gives quantum computers an exponential speed-up over classical computers for certain types of problems.

However, there’s a catch: when you measure a qubit in superposition, it collapses into one of the two definite states, $| 0 \rangle$ or $| 1 \rangle$ . This collapse is probabilistic, meaning we can only predict the probability of obtaining a specific outcome. This inherent randomness introduces challenges in designing quantum algorithms.

Dirac Notation

To describe and manipulate quantum states mathematically, we use Dirac notation. This notation employs “bras” and “kets” to represent quantum states and their complex conjugates, respectively.

Ket: A ket, denoted as $| a \rangle$ , represents a column vector: (where $a_1$ and $a_2$ are complex numbers)

\[| a \rangle = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} \]

Bra: A bra, denoted as $\langle b|$ , is the complex conjugate transpose of a ket: (where $b_1^∗$ and $b_2^∗$ are the complex conjugates of $b_1$ and $b_2$ )

\[\langle b| = |b\rangle^\dagger = \begin{pmatrix} b_1 \\ b_2 \end{pmatrix}^\dagger = \begin{pmatrix} b_1^* & b_2^* \end{pmatrix}\]

Inner and Outer Products

Combining bras and kets allows us to perform operations on quantum states:

Bra-ket (inner product): 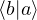$\langle b | a \rangle$ results in a complex number and represents the overlap between two states:

\[\langle b | a \rangle = a_1 b_1^* + a_2 b_2^* = \langle a | b \rangle^* \in \mathbb{C}\]

Ket-bra (outer product): 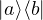$| a \rangle \langle b |$ results in a matrix and represents a linear transformation:

\[| a \rangle \langle b | = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} \begin{pmatrix} b_1^* & b_2^* \end{pmatrix} = \begin{pmatrix} a_1 b_1^* & a_1 b_2^* \\ a_2 b_1^* & a_2 b_2^* \end{pmatrix}\]

Orthogonality and Normalization

Two states are orthogonal if their inner product is zero, signifying they have no overlap. For example, the basis states $| 0 \rangle$ and $| 1 \rangle$ are orthogonal:

\[| 0 \rangle = \begin{pmatrix} 1 \\0 \end{pmatrix}, | 1 \rangle = \begin{pmatrix} 0 \\1 \end{pmatrix}, \langle 0 | 1 \rangle = 1 \cdot 0 + 0 \cdot 1 = 0\]

A crucial requirement for any quantum state is normalization. This means the total probability of finding the qubit in any of its possible states must equal 1. Mathematically, this is expressed as:

\[\langle \Psi | \Psi \rangle = 1, \: \text{e.g.} \: | \Psi \rangle = \frac{1}{\sqrt{2}}(| 0 \rangle+| 1 \rangle)=\begin{pmatrix} 1/\sqrt{2} \\1/\sqrt{2} \end{pmatrix} \]

Projective Measurement:

To measure a quantum state, we choose a set of orthogonal basis states. The measurement process projects the state onto one of these basis states.
The basis states are the eigenstates of the measurement operator. The most common measurement is the Z-measurement, which uses the computational basis states { $| 0 \rangle$ , $| 1 \rangle$ }.
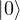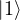Other common bases include the X-basis ({ 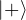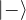$| + \rangle$ , $| - \rangle$ }) and the Y-basis ({ $| +i \rangle$ , $| -i \rangle$ })

\[\{| + \rangle = \frac{1}{\sqrt{2}}(| 0 \rangle+| 1 \rangle), \:\: | – \rangle = \frac{1}{\sqrt{2}}(| 0 \rangle-| 1 \rangle)\}\] \[\{| +i \rangle = \frac{1}{\sqrt{2}}(| 0 \rangle+i| 1 \rangle), \:\: | -i \rangle = \frac{1}{\sqrt{2}}(| 0 \rangle-i| 1 \rangle)\}\]

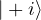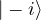Born Rule

The Born rule provides a way to calculate the probability of a quantum state collapsing to a particular basis state during measurement. Specifically, the probability $P(x)$ of the state $| \Psi \rangle$ collapsing onto the basis $\{| x \rangle, | x^\dagger \rangle\}$ to the state $| x \rangle$ is given by:

\[P(x) = |\langle x | \Psi \rangle|^2, \:\:\: \sum_iP(x_i) = 1 \]

e.g. $| \Psi \rangle = \frac{1}{\sqrt{3}}(| 0 \rangle+\sqrt{2}| 1 \rangle)$ is measurement in the basis $\{| 0 \rangle, | 1 \rangle \}$

\[P(0) = |\langle 0 | \frac{1}{\sqrt{3}}(| 0 \rangle+\sqrt{2}| 1 \rangle) \rangle|^2=| \frac{1}{\sqrt{3}}\langle 0 | 0 \rangle+\sqrt{\frac{2}{3}}\langle 0 | 1 \rangle|^2=\frac{1}{3}, \:\:\: P(1) = \frac{2}{3}\]

e.g. $| \Psi \rangle = \frac{1}{\sqrt{2}}(| 0 \rangle-| 1 \rangle)$ is measurement in the basis $\{| + \rangle, | - \rangle \}$

\[P(+) = |\langle + | \frac{1}{\sqrt{2}}(| 0 \rangle-| 1 \rangle)|^2=| \frac{1}{\sqrt{2}}(| 0 \rangle+| 1 \rangle). \frac{1}{\sqrt{2}}(| 0 \rangle-| 1 \rangle)|^2=\frac{1}{4}(\langle 0 | 0 \rangle-\langle 0 | 1 \rangle+\langle 1 | 0 \rangle-\langle 1 | 1 \rangle)=0, \:\: P(-)=1\]

Bloch Sphere

The Bloch sphere is a visual representation of a qubit’s state. Any normalized pure state can be represented as a point on the surface of a sphere with radius 1. A general state $| \Psi \rangle$ can be expressed in terms of two angles, $\theta$ and $\varphi$ , where $\theta \in [0,\pi]$ determines the probability of measuring $| 0 \rangle$ or $| 1 \rangle$ $(P(| 0 \rangle)=\cos^2\frac{\theta}{2}, P(| 1 \rangle)=1-\cos^2\frac{\theta}{2}=\sin^2\frac{\theta}{2})$ . $\varphi \in [0,2\pi]$ represents the relative phase between the two states.:

\[| \Psi \rangle = \cos \frac{\theta}{2} | 0 \rangle + e^{i \varphi} \sin \frac{\theta}{2} | 1 \rangle\]

Note: $\theta$ Zenith Angle: the angle measured from the positive Z-axis of the Bloch sphere to the qubit state vector. $\varphi$ Azimuthal Angle: the angle measured counterclockwise in the X-Y plane from the positive X-axis to the projection of the qubit state vector.

Each point on the Bloch sphere has corresponding coordinates given by the Bloch vector:

\[\vec{r} = \begin{pmatrix} \sin \theta \cos \varphi\\ \sin \theta \sin \varphi\\ \cos \theta \end{pmatrix}\]

e.g.

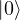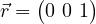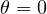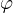$|0 \rangle$ state, State: This is the “north pole” of the Bloch sphere, representing the classical bit 0. Bloch vector, $\vec{r} = \begin{pmatrix} 0 \ 0 \ 1 \end{pmatrix}$ . $\theta = 0$ and $\varphi$ = undefined (since there’s no component in the X-Y plane).
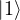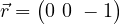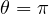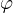$|1 \rangle$ state, State: This is the “south pole” of the Bloch sphere, representing the classical bit 1. Bloch vector, $\vec{r} = \begin{pmatrix} 0 \ 0 \ -1 \end{pmatrix}$ . $\theta = \pi$ and $\varphi$ = undefined (since there’s no component in the X-Y plane).
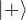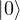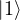$|+ \rangle$ state, State: This is an equal superposition of $| 0 \rangle$ and $| 1 \rangle$ , with no relative phase. It lies on the positive X-axis of the Bloch sphere. Bloch vector, 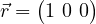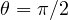$\vec{r} = \begin{pmatrix} 1 \ 0 \ 0 \end{pmatrix}$ . $\theta = \pi/2$ and $\varphi = 0$ .
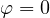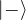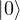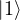$|- \rangle$ state, State: This is also an equal superposition of $| 0 \rangle$ and $| 1 \rangle$ , but with a relative phase of 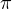$\pi$ . It lies on the negative X-axis. Bloch vector, 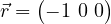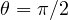$\vec{r} = \begin{pmatrix} -1 \ 0 \ 0 \end{pmatrix}$ . $\theta = \pi/2$ and $\varphi = \pi$ .
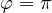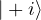$|+i \rangle$ state, State: This is an equal superposition with a relative phase of 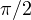$\pi/2$ . It lies on the positive Y-axis. Bloch vector, 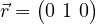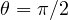$\vec{r} = \begin{pmatrix} 0 \ 1 \ 0 \end{pmatrix}$ . $\theta = \pi/2$ and $\varphi = \pi/2$ .
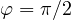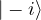$|-i \rangle$ state, State: Equal superposition with a relative phase of 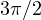$3\pi/2$ . It lies on the negative Y-axis. Bloch vector, 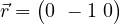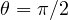$\vec{r} = \begin{pmatrix} 0 \ -1 \ 0 \end{pmatrix}$ . $\theta = \pi/2$ and $\varphi = 3\pi/2$ .
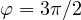General state. State: Consider the state, $| \Psi \rangle=(\frac{\sqrt{3}}{2})| 0 \rangle + (\frac{1}{2}e^{i\pi/3})| 1 \rangle$

\[\vec{r} = \begin{pmatrix} \sqrt{3}/2 \cdot \cos(\pi/3) \\ \sqrt{3}/2 \cdot \sin(\pi/3) \\ 1/2 \end{pmatrix} = \begin{pmatrix} \sqrt{3}/4 \\ 3/4 \\ 1/2 \end{pmatrix}\]