Blog

What Is a Unitary Matrix?

1️⃣ Intuition First

A unitary matrix represents a transformation that:

✔ Rotates or reflects vectors
✔ Does not stretch or shrink them
✔ Preserves total probability

Think of it like this:

A unitary operation moves a quantum state around in its space, but never distorts its length.

This is crucial because quantum states must always remain normalized.

2️⃣ Why Quantum States Must Be Preserved

A quantum state:

|\psi\rangle = \begin{bmatrix}\alpha \ \beta\end{bmatrix}

must satisfy:

|\alpha|^2 + |\beta|^2 = 1

If a transformation changed this length:

  • probabilities would no longer sum to 1
  • physics would break

👉 Unitary matrices are exactly the transformations that preserve length in complex vector spaces.

3️⃣ Formal Definition (Now the Math)

A matrix (U) is unitary if:

U^\dagger U = U U^\dagger = I

Where:

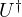  • (U^\dagger) = conjugate transpose of (U)
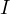  • (I) = identity matrix

Conjugate transpose means:

  1. Take the transpose
  2. Take complex conjugate of each entry

4️⃣ Simple Example (Hadamard Gate)

H = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}

Compute:

H^\dagger H = I

So Hadamard is unitary.

What does it do?

|0\rangle \xrightarrow{H} \frac{|0\rangle + |1\rangle}{\sqrt{2}}

It creates superposition without changing total probability.

5️⃣ Geometric Meaning (Very Important)

Image

On the Bloch sphere:

  • Unitary matrices correspond to rotations
  • No stretching, no shrinking
  • Every valid quantum gate is a rotation (or reflection)

📌 Key insight

Quantum computation is geometry in complex space.

6️⃣ What Unitary Is NOT

❌ Not any matrix
❌ Not allowed to scale vectors
❌ Not allowed to lose information

Example of non-unitary matrix:

\begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix}

This stretches vectors → invalid for quantum evolution.

7️⃣ Why All Quantum Gates Are Unitary

Quantum evolution follows Schrödinger’s equation, which guarantees:

✔ Reversibility
✔ Probability conservation
✔ Deterministic evolution before measurement

All of these imply:

\text{Evolution} \Rightarrow \text{Unitary transformation}

8️⃣ Unitary Matrices in Quantum Machine Learning

Now connect this directly to QML.

Classical ML

x \rightarrow Wx + b

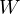  • (W): arbitrary matrix
  • Can shrink, expand, discard information

Quantum ML

|\psi\rangle \rightarrow U(\theta)|\psi\rangle

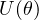  • (U(\theta)): unitary
  • Parameters (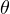\theta) are trainable
  • No information loss until measurement

📌 Very important difference

Learning in QML happens under unitary constraints, not arbitrary linear maps.

9️⃣ Why Measurement Is Needed

Because unitary operations are:

  • Linear
  • Reversible
  • Norm-preserving

They cannot:

  • create nonlinearity
  • discard information

👉 Measurement:

  • collapses the state
  • introduces nonlinearity
  • produces classical outputs

This is why measurement plays the role of activation functions in QML.

10️⃣ One-Sentence Summary

A unitary matrix is a complex linear transformation that preserves vector length and probability, making it the only physically allowed operation for quantum evolution.

Tags:

Leave a Reply