Why Part 0 Matters
Quantum Machine Learning (QML) is often presented as something mysterious or futuristic. In reality, it is a natural extension of classical machine learning into quantum state spaces.
Before discussing algorithms, speedups, or applications, we must understand what replaces vectors, layers, weights, and nonlinearities in a quantum setting. This part establishes the conceptual and mathematical foundations required to understand why QML works at all.
0.1 A Common Mathematical Language: Linear Algebra
Both machine learning and quantum computing are fundamentally based on linear algebra.
In classical machine learning:
Data is represented as vectors:
![]()
Models are functions parameterized by matrices and vectors:
![]()
Learning means adjusting parameters to minimize a loss.
In quantum computing:
Information is represented as state vectors:
![]()
Computation is performed via linear transformations:
![]()
where (U) is a unitary matrix. (read more here)
📌 Key observation
Both paradigms manipulate vectors using matrices. The difference lies in:
- the space (real vs complex),
- the constraints (unitary vs arbitrary),
- and how outputs are extracted (measurement vs direct readout).
This shared foundation is what makes QML possible.
0.2 Classical Bits and Quantum Qubits
Classical Bit
A classical bit can take only one of two values:
![]()
At any instant, the bit is in a definite state.
Quantum Qubit
A qubit, by contrast, exists in a superposition of basis states:
![]()
with the normalization condition:
![]()
- (
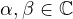 ) are probability amplitudes
) are probability amplitudes - Measurement yields:
- outcome (
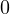 ) with probability (
) with probability (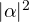 )
) - outcome (
 ) with probability (
) with probability (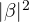 )
)
📌 Important distinction
A qubit is not “partly 0 and partly 1” in a classical sense.
It is a vector in a complex vector space, and probabilities emerge only upon measurement.
0.3 Geometric Interpretation: The Bloch Sphere
Any pure qubit state can be written as:
![]()
This maps to a point on the Bloch sphere:
- North pole → (
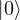 )
) - South pole → (
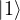 )
) - Equator → equal superpositions
🧠 Machine learning intuition
A single qubit can encode continuous information, similar to a real-valued feature, but constrained to lie on a sphere.
0.4 Multi-Qubit Systems and Tensor Products
When combining qubits, we use the tensor product.
Two-qubit state:
![]()
This state lives in a 4-dimensional complex space.
| Number of qubits | Dimension |
|---|---|
⚠️ This exponential growth is often misunderstood.
📌 Crucial point
The system exists in a ![]() -dimensional space, but measurement reveals only limited information.
-dimensional space, but measurement reveals only limited information.
This is why QML is powerful—but not trivially exploitable.
0.5 Tensor Products of Operators: Understanding (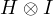 )
)
Quantum gates also combine via tensor products.
![]()
means:
- Apply Hadamard (H) to the first qubit
- Apply identity (I) to the second qubit
In matrix form:
![]()
🧠 ML analogy
This is analogous to transforming one feature while leaving another unchanged.
0.6 Entanglement: Beyond Classical Correlations
Separable (non-entangled) state:
![]()
Entangled state (Bell state):
![]()


This state cannot be written as a tensor product of two single-qubit states.
📌 Why this matters for QML
- Classical ML models interactions using extra parameters
- Quantum models generate non-factorizable feature interactions naturally
Entanglement acts as a built-in inductive bias for modeling complex dependencies.
0.7 Quantum Gates as Trainable Parameters
Quantum gates are unitary transformations:
![]()
Of special importance are parameterized rotation gates:
![]()
Example:
![]()
📌 In QML:
- These (
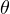 ) values are learnable parameters
) values are learnable parameters - They play the same role as weights in neural networks
0.8 Measurement as the Source of Nonlinearity
Quantum evolution is strictly linear:
![]()
However, measurement produces nonlinear classical outputs:
![]()
where (O) is an observable (e.g., Pauli-Z).
🧠 Critical insight
Measurement replaces activation functions.
Without measurement, quantum circuits alone cannot perform learning.
0.9 The Hybrid Quantum–Classical Learning Paradigm
Modern QML models are hybrid systems:
Classical data → Quantum encoding
→ Parameterized quantum circuit
→ Measurement
→ Classical loss + optimizer
→ Parameter update- Quantum computer: evaluates complex functions
- Classical computer: performs optimization
This is not a limitation—it is a design principle.
Summary of Part 0
By the end of Part 0, we have established:
✔ QML is linear algebra on quantum states
✔ Qubits generalize classical features
✔ Entanglement encodes complex feature interactions
✔ Trainable gates replace weights
✔ Measurement provides nonlinearity
