How Do We Do Measurement in Quantum Computing?

1️⃣ What Measurement Means (Intuition)

A quantum state:

$|\psi\rangle = \alpha|0\rangle + \beta|1\rangle$

does not have a definite value.

👉 Measurement asks a question:

“If I observe this system in a certain basis, what outcome do I get?”

The act of measurement:

Produces a classical number
Destroys the quantum state
Is probabilistic

2️⃣ Measurement Postulate (Formal Rule)

When you measure a state ( $|\psi\rangle$ ):

Possible outcomes

Each outcome corresponds to a basis state

Probability of outcome (i)

$P(i) = |\langle i | \psi \rangle|^2$

State after measurement

If outcome (i) is observed:

$|\psi\rangle \rightarrow |i\rangle$

📌 This is called state collapse.

3️⃣ Measurement in the Computational (Z) Basis

The most common measurement is in the computational basis:

${|0\rangle, |1\rangle}$

Example:

$|\psi\rangle = \sqrt{0.3}|0\rangle + \sqrt{0.7}|1\rangle$

Probability of measuring 0 → 0.3
Probability of measuring 1 → 0.7

After measurement, the state becomes either:

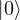( $|0\rangle$ ) or
( $|1\rangle$ )

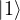4️⃣ Measurement as an Operator (Projective Measurement)

Each outcome has a projector:

$P_0 = |0\rangle\langle 0|, \quad P_1 = |1\rangle\langle 1|$

Probability:

$P(0) = \langle \psi | P_0 | \psi \rangle$

This formulation is extremely important for QML.

5️⃣ Expectation Value (What QML Actually Uses)

In machine learning, we usually do not care about single-shot outcomes.

Instead, we compute an expectation value.

Observable (example: Pauli-Z)

$Z = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}$

Expectation value:

$\langle Z \rangle = \langle \psi | Z | \psi \rangle$

This gives a continuous value between ([-1, 1]).

📌 This is the output of a quantum model.

6️⃣ Why Expectation Values Are Crucial for QML

Single Measurement	Expectation Value
Random (0 or 1)	Smooth, deterministic
High variance	Stable
Useless for training	Trainable output

🧠 Key insight

QML models learn by matching expectation values to labels.

7️⃣ How Expectation Values Are Estimated (Shots)

Quantum hardware gives random samples.

Procedure:

Run the circuit
Measure → get 0 or 1
Repeat (N) times (shots)
Average the results

$\langle Z \rangle \approx \frac{1}{N}\sum_{i=1}^N z_i$

Where:

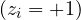$(z_i = +1)$ if outcome 0
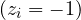$(z_i = -1)$ if outcome 1

8️⃣ Measuring Multiple Qubits

For two qubits, we measure operators like:

$Z \otimes Z$

Possible outcomes:

00, 01, 10, 11

Expectation value:

$\langle Z \otimes Z \rangle$

📌 This captures correlations, not just individual values.

9️⃣ Measurement Bases (X, Y, Z)

You are not restricted to Z-basis.

Basis	How
Z	Measure directly
X	Apply Hadamard → measure Z
Y	Apply (S^\dagger H) → measure Z

🧠 ML interpretation
Changing measurement basis = extracting different features.

10️⃣ Measurement in Variational Quantum Circuits (QML)

A typical QML model does:

$x \rightarrow |\psi(x)\rangle \xrightarrow{U(\theta)} |\psi(x,\theta)\rangle$

Prediction:

$\hat{y} = \langle \psi(x,\theta) | O | \psi(x,\theta) \rangle$

Loss:

$L(y, \hat{y})$

11️⃣ Why Measurement Is Nonlinear (Very Important)

Quantum evolution:

$|\psi\rangle \rightarrow U|\psi\rangle$

(linear)

Measurement:

$|\psi\rangle \rightarrow \text{probabilities}$

(non-linear)

👉 This is the only source of nonlinearity in QML.

12️⃣ One-Paragraph Summary

Quantum measurement converts a quantum state into classical information by probabilistically projecting it onto a basis state. In quantum machine learning, we do not rely on single measurement outcomes but instead estimate expectation values of observables by repeated measurements. These expectation values serve as model outputs, enabling loss computation and training through classical optimization.