What entanglement really means (beyond the buzzword)
Entanglement is not just correlation.
It is a non-classical correlation where:
The quantum state of the whole system is well-defined,
but the states of the individual qubits are not.
🔹 Start from separable (non-entangled) states
If two qubits are independent, their joint state can be written as:
![]()
Example:![]()
Here:
- Qubit A has its own state
- Qubit B has its own state
- Knowing A tells you nothing about B
🔹 Create entanglement using a circuit
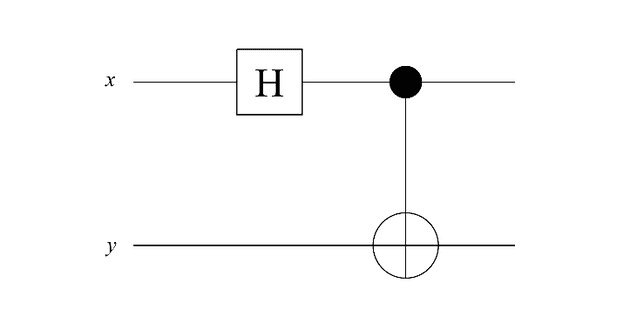
Canonical entanglement circuit:
![]()
Apply the Hadamard gate (H) to the first qubit, and do nothing (identity) to the second qubit.
Here:
- (H) = Hadamard gate
- (I) = Identity gate (no change)
- (
 ) = tensor (Kronecker) product
) = tensor (Kronecker) product
🧠 Intuition (before math)
Think of a two-qubit system:
| Qubit | Gate applied |
|---|---|
| Qubit 1 | Hadamard (H) |
| Qubit 2 | Identity (I → unchanged) |
So ( ![]() ) is a two-qubit operation, even though only one qubit is actively modified.
) is a two-qubit operation, even though only one qubit is actively modified.
🧮 Matrix form (why tensor product is needed)
Single-qubit matrices
![]()
Tensor product ( 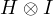 )
)
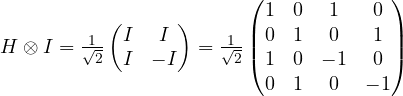
This is a 4×4 matrix because it acts on two qubits.
🎯 Action on basis states (this is the key)
Let’s apply ( ![]() ) to all computational basis states.
) to all computational basis states.
1️⃣ On ( 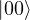 )
)
![]()
![]()
2️⃣ On ( )
)
![]()
3️⃣ On (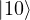 )
)
![]()
4️⃣ On ( )
)
![]()
🔁 Why this matters in entanglement
In the Bell-state circuit:
![]()
Key point:
- (
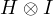 ) creates superposition
) creates superposition  turns superposition into entanglement
turns superposition into entanglement
Without (![]() ),
), ![]() alone cannot create entanglement.
alone cannot create entanglement.
📌 Circuit diagram interpretation

🔹 Why this state is entangled
Try to factor it:
![]()
👉 Impossible.
This is the defining property of entanglement. For more details read here: Link
