Quantum computing harnesses the unique laws of quantum mechanics to perform calculations in ways that are impossible for classical computers. At the core of quantum computation is the quantum circuit model , a sequence of fundamental operations called quantum gates.
From Classical Bits to Quantum Qubits
Before diving into circuits, it’s essential to understand the basic unit of quantum information: the qubit.
- Classical Bits are definite states, either “0” or “1”.
- Qubits can exist in a superposition, meaning they are simultaneously in both the “0” and “1” states. This superposition allows calculations to be performed on many states at once.
However, this advantage comes with a caveat: once a superposition state is measured, it collapses to one of its basis states (either ![]() or
or ![]() ).
).
Quantum states are typically described using Dirac notation:
- Ket notation, like
 , represents a quantum state vector (a column vector).
, represents a quantum state vector (a column vector). - The fundamental basis states are
 .
.
Any single qubit state ![]() can be visualized as a point on the surface of the Bloch sphere. The north pole represents
can be visualized as a point on the surface of the Bloch sphere. The north pole represents ![]() and the south pole represents
and the south pole represents ![]() . For more details see: Link1 and Link2
. For more details see: Link1 and Link2
Single-Qubit Gates: The Quantum Equivalent of NOT
In the circuit model, gates carry out elementary computations. A key distinction from classical logic is that quantum theory is unitary, meaning quantum gates must be represented by unitary matrices (where ![]() ). This makes quantum gates inherently reversible.
). This makes quantum gates inherently reversible.
Here are some of the most important single-qubit gates:
1. Pauli Gates ( )
)
These matrices form a basis for ![]() matrices, and any 1-qubit rotation can be written as their linear combination.
matrices, and any 1-qubit rotation can be written as their linear combination.
- Pauli-X Gate (
 ):
):
- Acts as a bit flip, equivalent to the classical NOT gate.
- It flips
 .
. - Matrix representation:
 .
.
- Pauli-Z Gate (
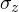 ):
):
- Acts as a phase flip.
- It leaves
 .
. - Matrix representation:
 .
.
- Pauli-Y Gate (
 ):
):
- Performs both a bit and phase flip.
- Matrix representation:
 .
.
2. Hadamard Gate (H)
The Hadamard gate is one of the most important gates for quantum circuits.
- Function: It creates a superposition.
- Use: It is used to change between the Z-basis
 .
. - Matrix representation:
 .
.
Two-Qubit Gates: Introducing Interaction and Entanglement
To process more complex information, we need gates that operate on multiple qubits, described using tensor products.
Controlled-NOT Gate (CNOT)
The CNOT gate is a crucial two-qubit gate. It is the reversible quantum analogue of the classical XOR gate.
- Operation: It has two inputs, a control qubit (
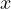 ) and a target qubit (
) and a target qubit (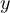 ).
).
- The control qubit
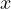 is unchanged.
is unchanged. - The target qubit
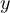 is flipped (NOT operation) if and only if the control qubit
is flipped (NOT operation) if and only if the control qubit 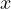 is
is 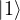 .
. - The output is
 .
. - For example:
 .
.
- The control qubit
- Matrix Representation:
 .
. - Circuit Diagram:

Entanglement: The Ultimate Quantum Correlation
The CNOT gate is essential for generating entanglement, a strong correlation between quantum systems.
A state ![]() on systems A and B is entangled if it cannot be written as a simple product of two separate states,
on systems A and B is entangled if it cannot be written as a simple product of two separate states, ![]() .
.
The four maximally entangled Bell states are a fundamental example and form an orthonormal basis. The first Bell state is created by applying an ![]() gate to the first qubit and a
gate to the first qubit and a ![]() gate to the pair, starting from
gate to the pair, starting from ![]() :
:
Read more here: Link
Quantum Teleportation
Entanglement is the key resource for quantum teleportation. This process allows Alice to send an unknown quantum state ![]() to Bob, even if she can only send two classical bits of information.
to Bob, even if she can only send two classical bits of information.
- Shared Entanglement: Alice and Bob must share a maximally entangled Bell state, such as
 .
. - Alice’s Measurement: Alice performs a Bell measurement on her qubit (S) and her half of the entangled pair (A).
- Classical Communication: Alice sends the classical results of her measurement (two bits,
 and
and 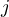 ) to Bob.
) to Bob. - Bob’s Operation: Based on Alice’s two bits, Bob applies a specific Pauli operation (
 ) to his qubit (B), which transforms his state into Alice’s original state
) to his qubit (B), which transforms his state into Alice’s original state  .
.
This powerful protocol demonstrates how quantum circuits—a combination of superposition, unitary gates, and entanglement—enable quantum information tasks.
Read more here: Link
