Blog

📡 Quantum Teleportation (Not Sci-Fi Transport!)

Image
Image
Image

First: what teleportation is not

❌ It does not move particles
❌ It does not send information faster than light
❌ It does not copy a quantum state

✅ It transfers an unknown quantum state using:

  • entanglement
  • measurement
  • classical communication

🧩 The Goal (in one line)

Alice has an unknown qubit
|\phi\rangle = \alpha|0\rangle + \beta|1\rangle

She wants Bob to end up with exactly the same state,
even though she does not know (\alpha,\beta).

🧠 The Resources (3 qubits)

QubitOwnerPurpose
SAliceState to teleport
AAliceHalf of entangled pair
BBobOther half

Alice and Bob pre-share entanglement:

|\Phi^+\rangle_{AB}=\frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)

🔗 Step 1: Initial combined state

The full 3-qubit system is:

|\Psi\rangle=|\phi\rangle_S\otimes|\Phi^+\rangle_{AB}=(\alpha|0\rangle + \beta|1\rangle)\otimes\frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)

At this point:

  • Bob’s qubit alone contains no information
  • Alice still fully owns the unknown state

🔄 Step 2: Alice applies quantum gates

Alice performs two operations:

1️⃣ CNOT (control = S, target = A)
2️⃣ Hadamard on qubit S

These gates entangle Alice’s qubits and rewrite the global state as:

\frac{1}{2}\sum_{i,j \in {0,1}}|ij\rangle_{SA}\otimes(\sigma_x^j \sigma_z^i |\phi\rangle_B)

👉 Key insight:
Bob’s qubit already contains the state ( |\phi\rangle ),
but it is scrambled by Pauli operators.

📏 Step 3: Alice measures (CRITICAL STEP)

Alice measures qubits S and A.

  • She gets two classical bits: ( (i,j) \in {00,01,10,11} )
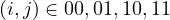  • Measurement destroys the original quantum state
  • No-cloning theorem is respected

After measurement:

  • Bob’s qubit collapses into one of:
    \sigma_x^j \sigma_z^i |\phi\rangle

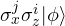
📞 Step 4: Classical communication

Alice sends the two classical bits ( (i,j) ) to Bob.

⚠️ This step:

  • is classical
  • obeys the speed of light
  • prevents faster-than-light communication

🔧 Step 5: Bob reconstructs the state

Bob applies a correction:

Alice’s bitsBob applies
00Identity
01( \sigma_x )
10( \sigma_z )
11( \sigma_x \sigma_z )

Result:
|\phi\rangle_B = \alpha|0\rangle + \beta|1\rangle

🎉 Teleportation complete

🧠 Why teleportation works (deep intuition)

IngredientRole
EntanglementShared quantum reference
MeasurementConverts quantum info → classical
Classical bitsTell Bob how to fix
Unitary gatesRestore the exact state

Entanglement supplies the quantum channel
Classical bits supply the instruction manual

🚫 Why teleportation doesn’t violate physics

❌ Faster-than-light?

No — Bob must wait for classical bits.

❌ Copying quantum states?

No — Alice’s state is destroyed during measurement.

❌ Sending energy or matter?

No — only information is reconstructed.

🧠 Summary

Quantum teleportation works by first sharing entanglement between two distant parties. Alice then performs a joint measurement on her unknown qubit and her half of the entangled pair, converting the quantum information into two classical bits. These bits instruct Bob which correction to apply to his qubit, allowing him to reconstruct the exact original quantum state. The original state is destroyed in the process, preserving the no-cloning principle and causality.

🧩 One-Line Intuition

Entanglement = shared quantum correlations
Teleportation = entanglement + measurement + 2 classical bits

Tags: ,

Leave a Reply