One of the first things people learn about qubits is that the basis states |0⟩ and |1⟩ are orthogonal.
Mathematically, this means:
Because of this, many beginners wonder:
“If |0⟩ and |1⟩ are orthogonal, why do textbooks place them at the north and south poles of the Bloch sphere instead of 90° apart?”
It’s a great question—and the answer reveals an important idea about how the Bloch sphere works.
🧠 1. The Bloch Sphere Is a Visualization Tool, Not a Literal Map of Hilbert Space
A qubit lives in a complex two-dimensional Hilbert space, but the Bloch sphere is a real three-dimensional picture we use to visualize it.
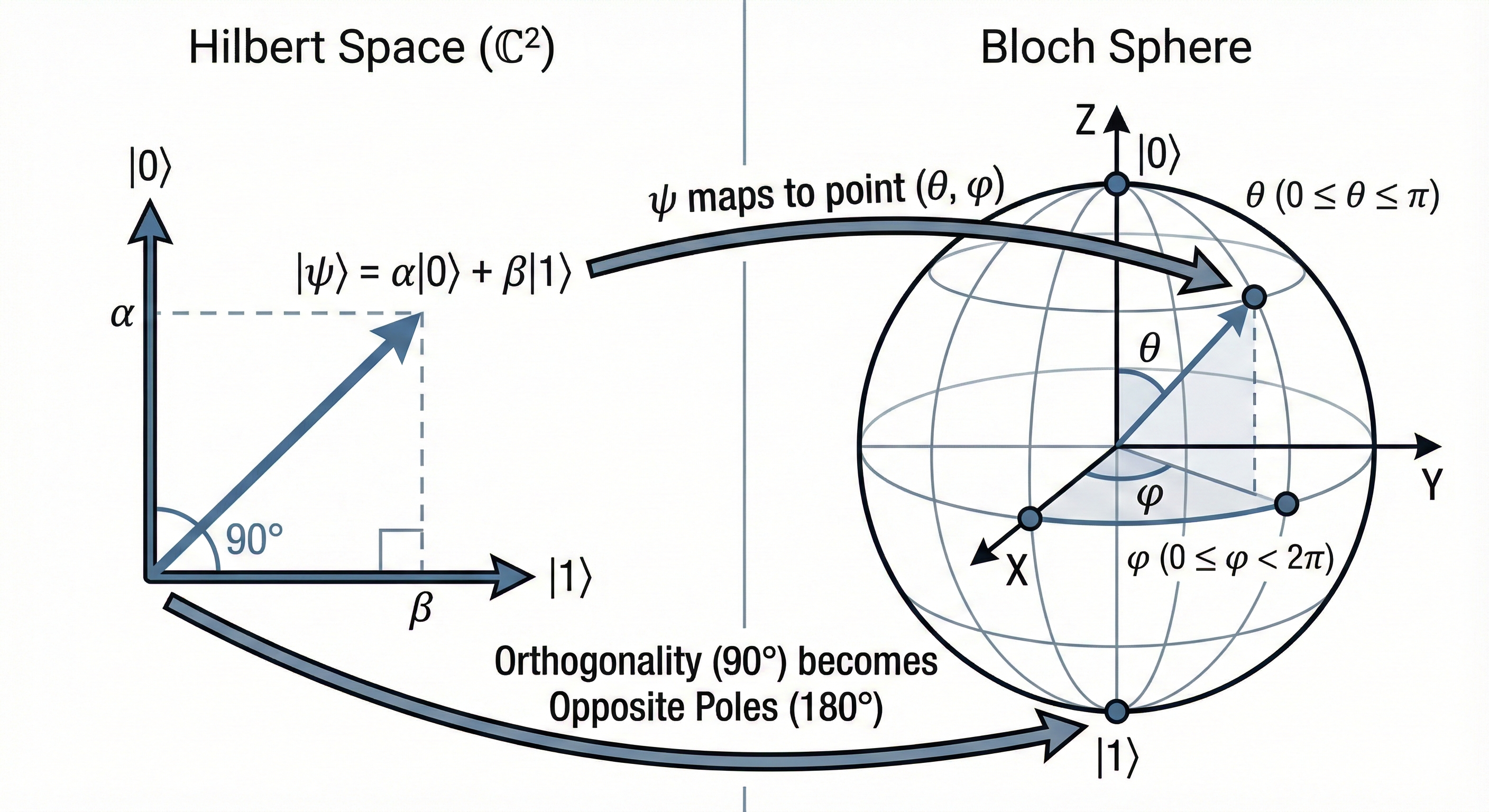
In this picture:
- |0⟩ is placed at the north pole,
- |1⟩ is placed at the south pole.
But this positioning does not mean they are “180° apart” in the Hilbert-space sense.
Rather, the Bloch sphere uses measurement behavior—not inner-product geometry—to place states.
🎯 2. Opposite Poles Represent Opposite Measurement Outcomes
When you measure a qubit in the computational basis:
- A qubit in |0⟩ is certain to give outcome 0.
- A qubit in |1⟩ is certain to give outcome 1.
Since their measurement outcomes are mutually exclusive, the Bloch sphere places them at opposite ends of the Z-axis.
This conveys a simple message:
Poles = states with completely opposite measurement probabilities.
So even though they are orthogonal mathematically, they appear visually as the most separated states.
📐 3. Orthogonality (90° in Hilbert Space) Becomes 180° on the Bloch Sphere
In Hilbert space, orthogonality corresponds to a 90° angle.
But the Bloch sphere does something different:
It maps a general qubit state
onto a point with spherical coordinates (θ, φ).
Under this mapping:
- |0⟩ → θ = 0° (north pole)
- |1⟩ → θ = 180° (south pole)
This is purely a visualization choice but one that makes measurement behavior intuitive.
🌐 4. Superposition Lives Everywhere Else on the Sphere
Once the poles are fixed, every other pure state falls somewhere on the sphere:
- Equal superposition → equator
- Phase differences → rotation around the equator
- Mixed states → inside the sphere
This makes the Bloch sphere a compact and beautiful way to visualize a qubit.
✅ In Simple Words
Here’s the intuition anyone can understand:
- |0⟩ and |1⟩ are orthogonal mathematically.
- But the Bloch sphere shows their measurement behavior, not their Hilbert-space angle.
- Opposite measurement outcomes → opposite poles.
That’s why they sit at the north and south poles.
