We say a two-qubit pure state is separable if it can be written as:
![]()
If this is impossible, the state is entangled.
✅ Method 1 (Most Direct): Factorization Test
Example: Bell state
![]()
Assume separability (proof by contradiction)
Assume:![]()
Expand RHS:![]()
Match coefficients with LHS:
| LHS | RHS | |
|---|---|---|
| (ac) | ||
| (ad) | ||
| (bc) | ||
| (bd) |
From zero terms:![]()
From non-zero terms:![]()
❌ These equations cannot all be satisfied simultaneously.
👉 Contradiction → state is entangled
✅ Method 2 (Cleaner & Powerful): Schmidt Decomposition
Theorem (Schmidt decomposition)
Any two-qubit pure state can be written as:![]()
- (
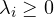 )
) - (
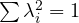 )
)
Key rule
| Schmidt rank | State type |
|---|---|
| 1 | Separable |
| ≥ 2 | Entangled |
Apply to Bell state
![]()
Schmidt coefficients:![]()
➡️ Schmidt rank = 2
➡️ Entangled
✔️ This is the standard textbook proof
✅ Method 3 (Physical Insight): Reduced Density Matrix Test
Step 1: Density matrix
![]()
Step 2: Partial trace over B
![]() ]
]
Step 3: Interpretation
- (
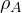 ) is mixed
) is mixed - But global state is pure
❗ A subsystem of a pure state is mixed only if the state is entangled
🧠 Intuition (Why separability fails)
- If separable → each qubit has its own definite state
- Bell state → individual qubits have no definite state
- Only the joint system is well-defined
📌 Summary Table
| Method | Rigor | Best use |
|---|---|---|
| Factorization | ★★★★☆ | Exams, simple states |
| Schmidt | ★★★★★ | Theory, papers |
| Density matrix | ★★★★★ | Mixed states, physics insight |
🧠 One-line takeaway
A state is entangled if it cannot be written as a tensor product — equivalently, if its Schmidt rank is greater than 1.
